
Private Key and Public Key Multiplication
Starting with a private key in the form of a randomly generated number k, we multiply it by a predetermined point on the curve called the generator point G to produce another point somewhere else on the curve, which is the corresponding public key K. The generator point is specified as part of the secp256k1 standard and is always the same for all keys in bitcoin.
K = k *G
where k is the private key, G is the generator point, and K is the resulting public key, a point on the curve. Since the generator point is always the same for all bitcoin users, a private key k multiplied with G will always result in the same public key K. The relationship between k and K is fixed, but can only be calculated in one direction, from k to K. That’s why a bitcoin address (derived from K) can be shared with anyone and does not reveal the user’s private key (k). A private key can be converted into a public key, but a public key cannot be converted back into a private key because the math only works one way.
Finding the Public Key
Implementing the elliptic curve multiplication above, we take the private key generated previously and multiply it by G: Multiply the private key k with the generator point G to find the public key K.
K = 1E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDD * G
Public Key K defined as a point K = (x,y).
K = (x, y)
where, x = F028892BAD…DC341A y = 07CF33DA18…505BDB
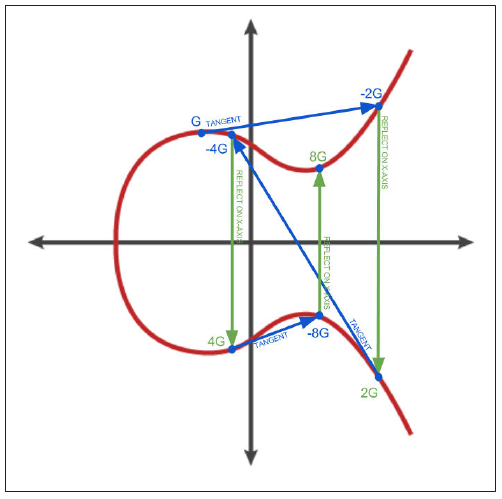
To visualize multiplication of a point with an integer, we will use the simpler elliptic curve over the real numbers — remember, the math is the same. Our goal is to find the multiple kG of the generator point G. That is the same as adding G to itself, k times in a row. In elliptic curves, adding a point to itself is the equivalent of drawing a tangent line on the point and finding where it intersects the curve again, then reflecting that point on the x-axis. The diagram below shows the process for deriving G, 2G, 4G, as a geometric operation on the curve.
Bitcoin Addresses
A bitcoin address is a string of digits and characters that can be shared with anyone who wants to send you money. Addresses produced from public keys consist of a string of numbers and letters, beginning with the digit “1”. Here’s an example of a bitcoin address:
1thMirt546nngXqyPEz532S8fLwbozud8
The bitcoin address is what appears most commonly in a transaction as the “recipient” of the funds. If we were to compare a bitcoin transaction to a paper cheque, the bitcoin address is the beneficiary, which is what we write on the line after “Pay to the order of ”. On a paper cheque, that beneficiary can sometimes be the name of a bank account holder, but can also include corporations, institutions or even cash. Because paper cheques do not need to specify an account, but rather use an abstract name as the recipient of funds, that makes paper cheques very flexible as payment instruments. Bitcoin transactions use a similar abstraction, the bitcoin address, to make them very flexible. A bitcoin address can represent the owner of a private/public key pair, or it can represent something else, such as a payment script, as we will see in “Pay to Script Hash (P2SH)” on page 134.
For now, let’s examine the simple case, a bitcoin address that represents, and is derived from, a public key. The bitcoin address is derived from the public key through the use of one-way cryptographic hashing; a “hashing algorithm” or simply “hash algorithm” is a one-way function that produces a fingerprint or “hash” of an arbitrary-sized input. Cryptographic hash functions are used extensively in bitcoin: in bitcoin addresses, in script addresses and in the mining “Proof-of-Work” algorithm. The algorithms used to make a bitcoin address from a public key are the Secure Hash Algorithm (SHA) and the RACE Integrity Primitives Evaluation Message Digest (RIPEMD), specifically SHA256 and RIPEMD160.
Starting with the public key K, we compute the SHA256 hash and then compute the RIPEMD160 hash of the result, producing a 160-bit (20-byte) number:
A = RIPEMD160(SHA256(K))
where K is the public key and A is the resulting bitcoin address. A bitcoin address is not the same as a public key. Bitcoin addresses are derived from a public key using a one-way function.
Base58 and Base58Check Encoding
Bitcoin addresses are almost always presented to users in an encoding called “Base58Check”, which uses 58 characters (a base-58 number system) and a checksum to help human readability, avoid ambiguity, and protect against errors in address transcription and entry. Base58Check is also used in many other ways in bitcoin, whenever there is a need for a user to read and correctly transcribe a number, such as a bitcoin address, a private key, an encrypted key, or a script hash.
Base-58 Encoding
In order to represent long numbers in a compact way, using fewer symbols, many computer systems use mixed-alphanumeric representations with a base (or radix) higher than 10.

For example, whereas the traditional decimal system uses the ten numerals 0 through 9, the hexadecimal system uses sixteen, with the letters A through F as the six additional symbols. A number represented in hexadecimal format is shorter than the equivalent decimal representation. Even more compact, Base-64 representation uses 26 lower-case letters, 26 capital letters, 10 numerals, and two more characters such as “+” and “/” to transmit binary data over text-based media such as email. Base-64 is most commonly used to add binary attachments to email.
Base-58 is a text-based binary encoding format developed for use in bitcoin and used in many other crypto-currencies. It offers a balance between compact representation, readability, and error detection and prevention. Base-58 is a subset of Base-64, using the upper and lower case letters and numbers but omitting some characters that are frequently mistaken for one another and can appear identical when displayed in certain fonts. Specifically, Base-58 is Base-64 without the 0 (number zero), O (capital o), l (lower L), I (capital i) and the symbols “+” and “/”. Or, more simply, it is a set of lower and capital letters and numbers without the four (0, O, l, I) mentioned above.
Bitcoin’s Base-58 Alphabet: 123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz
Base58Check Encoding
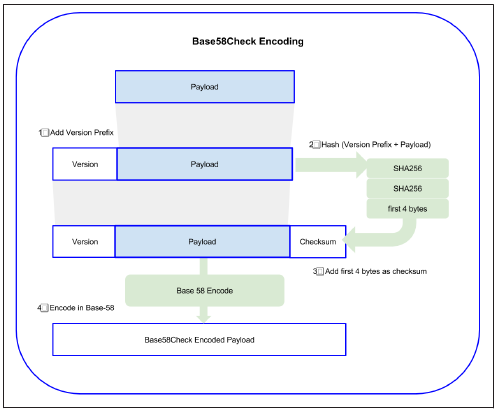
To add extra security against typos or transcription errors, Base58Check is a Base-58 encoding format, frequently used in bitcoin, which has a built-in error-checking code. The checksum is an additional four bytes added to the end of the data that is being encoded. The checksum is derived from the hash of the encoded data and can therefore be used to detect and prevent transcription and typing errors. When presented with a Base58Check code, the decoding software will calculate the checksum of the data and compare it to the checksum included in the code. If the two do not match, that indicates that an error has been introduced and the Base58Check data is invalid. For example, this prevents a mistyped bitcoin address from being accepted by the wallet software as a valid destination, an error which would otherwise result in loss of funds.
To convert data (a number) into a Base58Check format, we first add a prefix to the data, called the “version byte”, which serves to easily identify the type of data that is encoded. For example, in the case of a bitcoin address the prefix is zero (0x00 in hex), whereas the prefix used when encoding a private key is 128 (0x80 in hex). A list of common version prefixes is shown below in Table 4-1. Next compute the “double-SHA” checksum, meaning we apply the SHA256 hash algorithm twice on the previous result (prefix and data):
checksum = SHA256(SHA256(prefix+data))
From the resulting 32-byte hash (hash-of-a-hash), we take only the first four bytes. These four bytes serve as the error-checking code, or checksum. The checksum is concatenated (appended) to the end.
The result of the above is now a prefix, the data, and a checksum. This result is encoded using the base-58 alphabet described in the section above.
In bitcoin, most of the data presented to the user is Base58Check encoded to make it compact, easy to read, and easy to detect errors. The version prefix in Base58Check encoding is used to create easily distinguishable formats, which when encoded in Base-58 contain specific characters at the beginning of the Base58Check encoded payload, making it easy for humans to identify the type of data that is encoded and how to use it. This is what differentiates, for example, a Base58Check encoded bitcoin address that starts with a “1” from a Base58Check encoded private key WIF format that starts with a “5”. Some example version prefixes and the resulting Base-58 characters are shown below.