Elliptic Curve Cryptography is a type of asymmetric or public-key cryptography based on the discrete logarithm problem as expressed by addition and multiplication on the points of an elliptic curve.
Below we see an example of an elliptic curve, similar to that used by bitcoin:
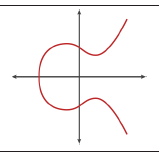
Bitcoin uses a specific elliptic curve and set of mathematical constants, as defined in a standard called secp256k1, established by the National Institute of Standards and Technology (NIST). The secp256k1 curve is defined by the following function, which produces an elliptic curve:
[ y^2 = \frac{x^3 + 7}{p} ]
or
[ y^2 \mod p = (x^3 + 7) \mod p ]
The mod p (modulo prime number p) indicates that this curve is over a finite field of prime order p, also written as ( \mathbb{F}_p ), where ( p = 2^{256} – 2^{32} – 2^{29} – 2^{28} – 2^{27} – 2^{26} – 2^{24} – 1 ), a very large prime number.
Because this curve is defined over a finite field of prime order instead of over the real numbers it looks like a pattern of dots scattered in two dimensions, which makes it difficult to visualize. However, the math is identical as that of an elliptic curve over the real numbers shown above. As an example, below is the same elliptic curve over a much smaller finite field of prime order 17, showing a pattern of dots on a grid. The secp256k1 bitcoin elliptic curve can be thought of as a much more complex pattern of dots on an unfathomably large grid.
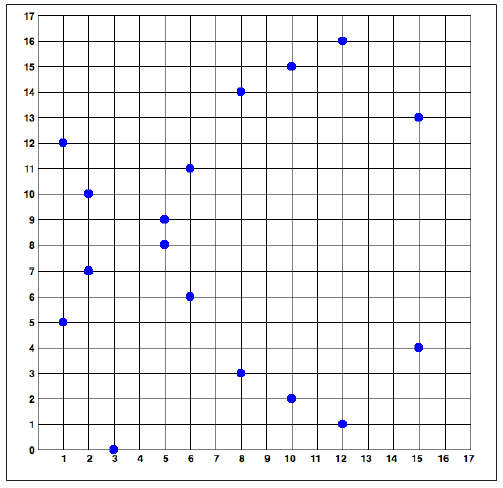
So for example, below is a point P with coordinates (x,y) that is a point on the secp256k1 curve. You can check this yourself using Python:
P = (55066263022277343669578718895168534326250603453777594175500187360389116729240,
32670510020758816978083085130507043184471273380659243275938904335757337482424)Python 3.4.0 (default, Mar 30 2014, 19:23:13)
[GCC 4.2.1 Compatible Apple LLVM 5.1 (clang-503.0.38)] on darwin
Type “help”, “copyright”, “credits” or “license” for more information.
p = 115792089237316195423570985008687907853269984665640564039457584007908834671663
x = 55066263022277343669578718895168534326250603453777594175500187360389116729240
y = 32670510020758816978083085130507043184471273380659243275938904335757337482424
(x ** 3 + 7 - y**2) % p
0In elliptic curve math, there is a point called the “point at infinity,” which roughly corresponds to the role of 0 in addition. On computers, it’s sometimes represented by x = y = 0 (which doesn’t satisfy the elliptic curve equation — but it’s an easy separate case that can be checked).
There is also an operator “+,” called “addition,” which has some properties similar to the traditional addition of real numbers that grade school children learn. Given two points P1 and P2 on the elliptic curve, there is a third point P3 = P1 + P2, also on the elliptic curve.
Geometrically, this third point P3 is calculated by drawing a line between P1 and P2. This line will intersect the elliptic curve in exactly one additional place. Call this point P3′ = (x, y). Then reflect in the X axis to get P3 = (x, -y).
There are a couple of special cases which explain the need for the “point at infinity.” If P1 and P2 are the same point, the line “between” P1 and P2 should extend to be the tangent on the curve at this point P1. This tangent will intersect the curve in exactly one new point. You can use techniques from calculus to determine the slope of the tangent line. These techniques curiously work even though we are restricting our interest to points on the curve with two integer coordinates!
In some cases (i.e., if P1 and P2 have the same x values but different y values), the tangent line will be exactly vertical, in which case P3 = “point at infinity.”
If P1 is the “point at infinity,” then the sum P1 + P2 = P2. Similarly, if P2 is the point at infinity, then P1 + P2 = P1. This shows how the point at infinity plays the role of 0.
It turns out that + is associative, which means that (A + B) + C = A + (B + C). That means we can write A + B + C without parentheses without any ambiguity.
Now that we have defined addition, we can define multiplication in the standard way that extends addition. For a point P on the elliptic curve, if k is a whole number, then kP = P + P + P + … + P (k times). Note that k is sometimes confusingly called an “exponent” in this case.